The first paragraph of Mr. Neptune's "discussion" fully states his opinions. The remainder of his review contains a series of mathematical errors, flawed arguments, and/or deliberate misstatements:
On
page 325 of SP-1237, in paragraph 1, Mr. Neptune
states "Equation (16), however, can not be used for the initial elastic-only
portion of dynamic crush (before the onset of residual crush,
f
) since the ratio
is zero.".
Equation (16) from SAE 97-0960 (page 321) is as follows:
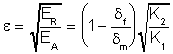
It is not clear what problem Mr. Neptune has with Equation
(16) when f /m
goes to zero. The only calculation 'problem' with equation (16) would
occur if 
= 0.0 (
i.e. where there is no maximum deformation, which occurs only when there
is no collision).
Obviously, from elementary mathematics,
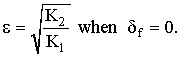
The "impossible" calculation results cited by
Mr. Neptune are the direct result of his incomprehensible rejection of
equation (16) for the case of 
=
0.
p. 324, paragraph 2: Figure
6A depicts the restitution coefficient for a specific defined set of inputs
rather than the overall general case. The infinite limit argument deliberately
ignores item 3 of Appendix 3.
p. 324, paragraphs 3 through 5: From equation (16),
= 
.
In the specific example in Figure 2,
> 1.00. Therefore, is
set to 1.000. Setting equal
to 1.000 in equation (1) yields 
=
1.000 for 
6.2
inches. No mystery. Simple mathematics.
The "not realistic" comments are not supported by any specific
identified evidence.
Neptune ignores item 7 of Appendix 3 which points out the fact that CRASH (EDCRASH) effectively assumes an elastic range, in terms of full dimensional recovery, equal to A/B. (For further clarification of this statement, please see Question#4 of "Questions related to 97-0960")
The proposed restitution model has an effective elastic
range, in terms of full dimensional recovery, equal to
which is smaller than that of EDCRASH (Equation (9)).
See item 5 of Appendix 3
for a discussion of "absorbed energy", "elastic" terminology.
p 325, paragraph 1: In Figure 13,
is
established by equation (16) to be 0.314. It makes no sense to set
equal
to a value larger than in
equation (1). The relationship between equations (1) and (16) that is defined
by Neptune is nonsense.
p 325, paragraph 2: SAE paper 940916, 1981 Ford Escort. A 50 mm tear in the top flange of the front bumper at V= 11.07 MPH. No damage to other front end components. 2.25 inch isolator compression (fully rebounded). Neptune apparently assumes no dynamic deformation other than the isolators.
p 325, paragraph 3: The complete omission of restitution effects in CRASH (EDCRASH) creates an ERROR equal to the magnitude of the ignored restitution effects.
p 325, paragraph 4: In any collection of SAE barrier
tests, compare the measured values of 
V
with the approach speeds.
p 325, paragraph 5: Neptune states that "The
restitution model needs to be reconfigured such that restitution is less
than, or equal to, the theoretical limit of 1.0 at zero dynamic crush and
decreases from that point as the dynamic crush increases". The suggestion
of a "reconfiguration" deliberately ignores item
4 of Appendix 3, the fact that is
presently limited to 
or 1.000, whichever is smaller.
Please also see our discussion of the SAE
Accident Reconstruction Session Review Process
We hope you read the 4 SAE papers we prepared with McHenry Consultants, Inc. for the 1997 SAE congress.
We welcome any questions, comments, corrections or requests for further information. We can be reached by e-mail at McHenry@McHenrySoftware.com